Test de Mantel en R

Actualización 1 (17/12/2018):
-Se explicó otro camino para graficar utilizando ggplot2
Actualización 2 (18/12/2018)
-Se añadió el valor del coeficiente de correlación (r) dentro del gráfico empleando ggplot2

En el día de hoy aprenderemos a hacer un test de correlación Mantel en R utilizando el paquete vegan.

¿En qué consiste este test? Básicamente lo que hace es estimar si hay o no correlación ya sea positiva o negativa entre dos conjuntos de datos de distancias (matrices). Por ejemplo: podemos probar si hay o no correlación entre la distancia genética y geográfica entre poblaciones de alguna especie (de esta manera se evalúa si hay aislamiento genético por distancia); o también podemos evaluar si existe o no correlación entre la disimilitud de comunidades biológicas y la distancia geográfica entre ellas.

Lo primero que debemos hacer es conocer cómo vamos a organizar los datos para introducirlos a R. Supongamos que tenemos 5 poblaciones (A-E) de Aedes albopictus. Entonces en teoría deberíamos considerar 10 comparaciones teóricas (5*(5-1)/2). Es importante que al momento de construir nuestra matriz coloquemos el mismo orden de las poblaciones tanto en la primer columna como en la primera fila (y que el orden sea igual en ambas matrices). Como verán así obtendremos una matriz cuadrada; y por supuesto, una matriz simétrica; ya que, al transponer las distancias de la segunda columna, estos serán equivalentes a los valores de la segunda fila. Los valores de la diagonal serán 0 (puesto que, la comparación se realiza entre la misma población). Veamos:

A B C D E
A  0 0.9 0.7 0.3 0.8
B 0.9 0 Terminen de rellenar ustedes... así le agarran el tiro ;)
C 0.7 0.5 0
D 0.3 0.1 0.7 0
E 0.8 0.2 0.6 0.3 0

Una vez entendido esto.. empecemos...

Para este ejemplo utilizaré unos datos compartidos por mi profesor de Ecología II para una práctica de laboratorio. Les explico rápidamente de qué van estos datos. Se tratan del muestreo de invertebrados asociados a 11 boñigas (cada boñiga es considerada como una comunidad). La pregunta es la siguiente: ¿La similitud de composición de especies depende de la distancia entre las boñigas?

Para esto se construyeron dos matrices (descargar acá):

1. Matriz de disimilitud (disim.txt) empleando el complemento del índice de Chao-Jaccard.
2. Matriz de distancia geográfica (geo.txt) entre las boñigas

#Una vez tengamos las matrices descargadas, procedemos a abrir R e instalamos el paquete:

install.package("vegan")

#Lo cargamos
library(vegan)

#Verificamos nuestro directorio de trabajo
getwd()
 "C:/Users/Admin/Documents"

#Copiamos las matrices y las pegamos en esa ruta

#Cargamos matrices:
geo <- read.table("geo.txt", header=T)
disimi <- read.table("disim.txt", header=T)  #El argumento header nos permite especificarle a la función que la primera fila y columna de nuestro archivo contienen los nombres de las variables


#Aquí ustedes ya pueden hacer el test, simplemente hacen esto:
test <- mantel(geo, disimi, method= "pearson", permutations= 1000) #Ustedes pueden elegir otro método, ya sea Kendall o Spearman. También pueden cambiar el número de permutaciones

Mantel statistic based on Pearson's product-moment correlation

Call:
mantel(xdis = distgeo, ydis = disimilitud, method = "pearson",      permutations = 1000)

Mantel statistic r: 0.3423 
      Significance: 0.031968

Upper quantiles of permutations (null model):
  90%   95% 97.5%   99%
0.198 0.296 0.355 0.423
Permutation: free
Number of permutations: 1000

 #Gráfico de dispersión#

#Primero le indicamos a R que nuestros datos cargados corresponden a matrices de distancia:
matrizgeo <- as.matrix(geo)
matrizsim <- as.matrix(disimi)

#Graficamos
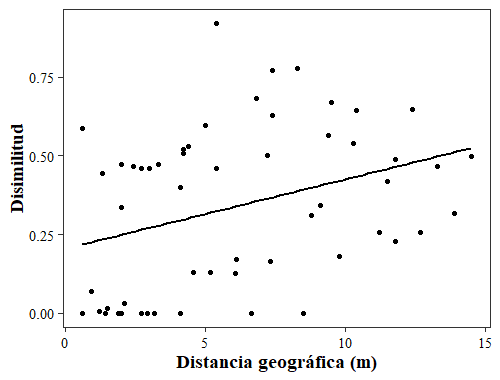
grafica <- plot(matrizgeo, matrizsim, pch=16, cex=1, col="black", xlab="Distancia geográfica (m)", ylab="Disimilitud de composición de especies")
grafica

#Obtendremos algo así:

Otro camino para graficar con ggplot2

Instalamos los siguientes paquetes: ggplot2 y extrafont (paquete empleado para cambiar las fuentes del gráfico)

install.packages("ggplot2")
install.packages("extrafont")

#Cargamos los paquetes
library(ggplo2)
library(extrafonts)

#Creamos un data frame para extraer los valores de las matrices, ya sea la fracción triangular superior o inferior (en este ejemplo, utilizaremos la inferior, es decir: lower)
df <- data.frame(Disimilitud=disimi[lower.tri(disimi)], Distancia=geo[lower.tri(geo)])

#Revisamos df
df

#¿Ven lo que hicimos? hemos organizado las variables de manera pareada (55 comparaciones en total)
##Comenzamos a graficar##
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point()

#Modificamos el tema por el tema theme_test; ajustamos tamaño de letra y fuente
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman")

#Modificamos los títulos de los ejes con la función labs
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud")

#Podemos ajustar el tipo de letra del título de los ejes (e.g. negrita)
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud") + theme(axis.title = element_text(face="bold"))

#Cambiamos el color de los valores de los ejes a negro (puede ser otro color) Click acá para ver el catálogo de colores en R
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud") + theme(axis.title = element_text(face="bold"), axis.text = element_text(colour="black"))

#Podemos añadir la línea de tendencia con la función geom_smooth
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud") + theme(axis.title = element_text(face="bold"), axis.text = element_text(colour="black")) + geom_smooth(method=lm)

#Si quieren remover el intervalo de confianza, modificamos el argumento "se" de la función geom_smooth
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud") + theme(axis.title = element_text(face="bold"), axis.text = element_text(colour="black")) + geom_smooth(method=lm, se=FALSE)

#Para ajustar el color, podemos emplear el argumento "color" de la misma función
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud") + theme(axis.title = element_text(face="bold"), axis.text = element_text(colour="black")) + geom_smooth(method=lm, se=FALSE, color="black")

#El ajuste del grosor de la línea de tendencia se ajusta con el argumento "size" de la misma función
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud") + theme(axis.title = element_text(face="bold"), axis.text = element_text(colour="black")) + geom_smooth(method=lm, se=FALSE, color="black", size=.5)

#Como la variable disimilitud va de 0 a 1, podemos ajustar el límite de su eje con la función ylim
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud") + theme(axis.title = element_text(face="bold"), axis.text = element_text(colour="black")) + geom_smooth(method=lm, se=FALSE, color="black", size=.5) + ylim(0,1)

#Para añadir el valor del coeficiente de correlación (r), empleamos la función annotate (le podemos modificar la fuente y el tamaño) observen que cuando ponemos el argumento parse como TRUE (T), le indicamos que estamos haciendo una anotación matemática y seguirá la sintaxis que utiliza ggplot para estas expresiones matemáticas (ver la sintaxis acá):
plot <- ggplot(df, aes(x=Distancia, y=Disimilitud)) + geom_point() + theme_test(base_size = 14, base_family = "Times New Roman") + labs(x="Distancia geográfica (m)", y="Disimilitud") + theme(axis.title = element_text(face="bold"), axis.text = element_text(colour="black")) + geom_smooth(method=lm, se=FALSE, color="black") + ylim(0,1) + annotate("text", x=13.5, y=1, label="italic(r)==0.3423", family = "Times New Roman", parse=T, size=5)

¡Listo! Estos serían los ajustes principales que se le pueden hacer al gráfico. Las dimensiones que utilicé para exportar fueron de 400 (Width) x 380 (Height).


El plus:

¿Cómo podemos interpretar todo este revoltijo?

Sencillo. El valor r es el coeficiente de correlación. Recordemos que este valor oscila entre -1 y 1. Este valor sólo nos indica la intensidad y orientación de la correlación (positiva o negativa) que estamos probando. Si el valor es negativo, nos está indicando que la correlación es negativa, es decir, es inversamente proporcional. En el sentido contrario, cuando el valor es positivo, la correlación es directamente proporcional. Entonces los escenarios posibles son:

A medida que aumenta la distancia geográfica aumenta la similitud de la composición de especies entre las boñigas (esto sería si la correlación fuera negativa). Sin embargo, nuestro coeficiente de correlación fue positivo (0.34323), y el nivel de significancia fue por debajo de 0.05 (0.031968). Esto nos permite concluir que, cuando aumenta la distancia geográfica entre las boñigas, la composición de especies entre estas es diferente (son menos similares).

Chan chan... hermos terminado. Espero les haya sido de utilidad.

Información genética básica de microsatélites utilizando diveRsity (+ Hardy-Weinberg)

En el día de hoy vamos a aprender a calcular algunos parámetros genéticos básicos (heterocigosis observada, esperada, equilibrio de Hardy-Weinberg, número de alelos, y riqueza alélica) de distintas poblaciones en función de microsatélites (marcadores moleculares codominantes). Para este ejemplo, vamos a tomar los datos publicados por Sun et al. 2013. Estos datos constan de 19 poblaciones asiáticas (n=916 individuos) de Homo sapiens, a las cuales se les realizó genotipificación en función de 10 loci (10 microsatélites).

Lo primero que debemos hacer es convertir la matriz suplementaria en formato Genepop (esto lo pueden hacer en Excel). Es importante mencionar que el formato Genepop se clasifica en dos tipos de acuerdo con el número de caracteres (dos o tres) que se emplean para definir un alelo. En este ejemplo, los alelos están definidos por tres caracteres. Por ejemplo:

                          Locus_1
Individuo 1      282283    (alelos 282 y 283).

El formato de Genepop de 3 caracteres sigue esta estructura:

Análisis de microsatélites de Homo sapiens #en la primera fila añaden el título de su trabajo o alguna anotación en particular#
Locus_1 #En estas filas definen los loci (recordemos que los datos de Sun et al. 2013 tienen 10 loci)#
Locus_2
Locus_3
Pop #Al colocar Pop en una fila, estamos definiendo la población#
Springfield_1 , 123123 456456 789789 #Cada columna de valores representa un loci, los loci están ordenados de la misma manera en cómo los ordenador arriba#
Springifield_2 , 122120 455456 798790 #Recuerden que 123123 significa que el individuo Springifield_1 tiene dos alelos 123 en el Locus_1#
Springfield_3 ,  123122 450459 799766 #Ojo, es importante colocar una coma después de cada individuo, para así delimitarlos de los alelos#
Pop
Fargo_1 , 122120 444450 780799
Fargo_2 , 123129 444459 781766
Fargo_3 , 120121 450459 799786
Pop
Albuquerque_1 , 125128 450455 781789
Albuquerque_2 , 123128 459484 792788
Albuquerque_3 , 128129 458457 799786

Ya, ya, sin tanta carreta, el formato debe quedar así:

Análisis de microsatélites de Homo sapiens
Locus_1
Locus_2
Locus_3
Pop
Springfield_1 , 123123 456456 789789
Springfield_2 , 122120 455456 798790
Springfield_3 ,  123122 450459 799766
Pop
Fargo_1 , 122120 444450 780799
Fargo_2 , 123129 444459 781766
Fargo_3 , 120121 450459 799786
Pop
Albuquerque_1 , 125128 450455 781789
Albuquerque_2 , 123128 459484 792788
Albuquerque_3 , 128129 458457 799786

El archivo lo deben guardar en formato ".txt". Acá pueden descargar el archivo formato Genepop que yo generé a partir de la matriz suplementaria (si alguien detecta algún error, por favor, informen).

Ahora que tenemos nuestro archivo en formato Genepop, pues a lo que vinimos:

Abrimos R, instalamos (en caso de que no lo tengan) y abrimos el paquete diveRsity

install.packages("diveRsity")
library(diveRsity)

#Abrimos el archivo y lo analizamos de una vez con la función divBasic#

divBasic(infile = NULL, outfile = NULL, gp = 3, bootstraps = NULL, HWEexact = FALSE, mcRep = 2000)

#Primero entendamos un poco la función con sus argumentos... #
#en el argumento infile, especificamos entre comillas el nombre del archivo de entrada Genepop#
#en el argumento outfile le estamos indicando a la función que nos exporte los resultados con un nombre determinado; el archivo de salida está en formato ".txt"#
#en el argumento gp, estamos especificando que los alelos están definidos por 3 caracteres#
#si argumento HWEexact es TRUE o T, la función realizará el análisis de equilibrio de Hardy-Weinberg para cada locus en cada una de las poblaciones, si no quieren hacer EHW coloquen F o FALSE#
#con el argumento bootstraps podemos definir el número de iteraciones#

divBasic("erre.txt", outfile = "resultados.txt", gp=3, bootstraps= 1000, HWEexact = TRUE)

Enter y chao es que te digo... :D

En nuestro directorio de trabajo se creará una carpeta con el nombre que especificamos en la función outfile ; una vez adentro encontraremos el archivo en formato ".txt" . Lo abren, y obtendrán sus jugosos resultados.

Mis documentos -> resultados-[diveRsity] -> [divBasic].txt

Les deberá aparecer algo como esto: (sólo saqué los resultados de una población)

Dai(Dehong

L1       L2 L3 L4           L5  L6 L7 L8 L9           L10 Overall

N          48              48              47             48             48             48             48             48              48            48     47.9

A          15               6               11             10              5              10              8                7               12            10       94

%         75              50            61.11        45.45        41.67        52.63        61.54  53.85         63.16       71.43   57.58

Ar       12.5           5.47 9.62          8.59          4.99          9.49          6.51           6.55         10.26         9.18    8.32

Ho        0.9           0.77            0.6            0.77          0.65          0.92          0.71           0.73           0.81         0.77    0.76

He        0.89  0.71 0.76          0.72          0.72           0.86         0.75            0.79           0.83         0.76    0.78

HWE   0.366          0              0.686         1              0.882          1             0.031          0.838         0.612       0.79    0.137

N: número de individuos evaluados por locus
A: Número de alelos observados por locus
%: Porcentaje de alelos totales observados por locus
Ar: Riqueza alélica por locus
Ho: Heterocigosis observada por locus
He: Heterocigosis esperada por locus
HWE: p-valores obtenidos del análisis de Hardy-Weinberg (recorderis: si el p-value < 0.05 (significancia estándar), indica que la hipótesis nula (los locus/poblaciones se encuentran en equilibrio Hardy-Weinberg) se rechaza, y se acepta que no están en equilibrio.


Espero esta mini-guía les sea de utilidad. Estoy abierto a cualquier sugerencia. Saludos.